Скаля́рний добу́ток (англ. dot product, scalar product ) — бінарна операція над векторами , результатом якої є скаляр .
Скалярний добуток Формула a ⋅ b = ∑ i a i b i {\displaystyle {\boldsymbol {a}}\cdot {\boldsymbol {b}}=\sum _{i}a_{i}b_{i}} [1] Позначення у формулі a ⋅ b {\displaystyle {\boldsymbol {a}}\cdot {\boldsymbol {b}}} a i {\displaystyle a_{i}} a {\displaystyle {\boldsymbol {a}}} b {\displaystyle {\boldsymbol {b}}} b i {\displaystyle b_{i}} Підтримується Вікіпроєктом Вікіпедія:Проєкт:Математика Скалярний добуток у Вікісховищі
Скалярний добуток геометричних векторів x → {\displaystyle {\vec {x}}} y → {\displaystyle {\vec {y}}}
x → ⋅ y → = | x → | | y → | cos ∡ ( x → , y → ) {\displaystyle {\vec {x}}\cdot {\vec {y}}=|{\vec {x}}|\,|{\vec {y}}|\,\cos \measuredangle \left({\vec {x}},{\vec {y}}\right)} де | x → | {\displaystyle |{\vec {x}}|} | y → | {\displaystyle |{\vec {y}}|} довжинами векторів , а cos ∡ ( x → , y → ) {\displaystyle \cos \measuredangle \left({\vec {x}},{\vec {y}}\right)} косинусу кута між цими векторами. Як і у випадку звичайного множення , знак множення можна не писати: x → ⋅ y → = x → y → {\displaystyle {\vec {x}}\cdot {\vec {y}}={\vec {x}}{\vec {y}}}
Два означення добутку векторів:
Скалярним добутком двох векторів називають число, рівне добутку довжин цих векторів на косинус кута між ними. Скалярним добутком двох векторів називають число, рівне добутку довжини одного з цих векторів на проєкцію іншого вектора на вісь, обумовлену першим з вказаних векторів (добуток довжини x → {\displaystyle {\vec {x}}} y → {\displaystyle {\vec {y}}} x → {\displaystyle {\vec {x}}} В лінійній алгебрі поняття скалярного добутку узагальнено. Так, скалярним добутком називають функцію, що зіставляє парі елементів векторного простору елемент з поля , над яким побудований векторний простір. Скалярний добуток двох векторів x {\displaystyle x} y {\displaystyle y} ⟨ x , y ⟩ {\displaystyle \langle x,y\rangle } x y {\displaystyle xy} x T y {\displaystyle x^{T}y} множенням матриць .
Взагалі кажучи, для векторного простору існують різні варіанти скалярного добутку. Простір із визначеним скалярним добутком позначають як передгільбертів простір .
Визначення в евклідовому просторі ред.
В лінійній алгебрі скалярний добуток двох векторів
x → = ( x 1 x 2 ⋮ x n ) {\displaystyle {\vec {x}}={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}} y → = ( y 1 y 2 ⋮ y n ) {\displaystyle {\vec {y}}={\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}} в ортонормованому базисі n {\displaystyle n}
x → ⋅ y → := ∑ i = 1 n x i y i = x 1 y 1 + x 2 y 2 + ⋯ + x n y n {\displaystyle {\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}x_{i}y_{i}={x_{1}}{y_{1}}+{x_{2}}{y_{2}}+\dotsb +{x_{n}}{y_{n}}} В загальному випадку: x → ⋅ y → := ∑ i = 1 n ∑ j = 1 n x i g i j y j = x 1 y 1 + x 2 y 2 + ⋯ + x n y n {\displaystyle {\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}\sum _{j=1}^{n}x_{i}g_{ij}y_{j}={x_{1}}{y_{1}}+{x_{2}}{y_{2}}+\dotsb +{x_{n}}{y_{n}}} g {\displaystyle g} Матриці Грама Наприклад, в тривимірному евклідовому просторі, скалярний добуток двох векторів обчислюється так:
( 1 2 3 ) ⋅ ( − 7 8 9 ) = 1 ⋅ ( − 7 ) + 2 ⋅ 8 + 3 ⋅ 9 = 36 {\displaystyle {\begin{pmatrix}1&2&3\end{pmatrix}}\cdot {\begin{pmatrix}-7\\8\\9\end{pmatrix}}=1\cdot (-7)+2\cdot 8+3\cdot 9=36} тобто для того, щоб отримати значення скалярного добутку, матрицю -стовпчик, яка відповідає першому зі співмножників треба транспонувати й помножити на матрицю-стовпчик другого вектора за правилами множення матриць.
Норма векторів ред. Завдяки скалярному добутку, можна так обчислити норму вектора :
| | x → | | = x → ⋅ x → {\displaystyle ||{\vec {x}}||={\sqrt {{\vec {x}}\cdot {\vec {x}}}}} Якщо простір евклідів, то:
| | x → | | = x → ⋅ x → = x 1 2 + x 2 2 + ⋯ + x n 2 {\displaystyle ||{\vec {x}}||={\sqrt {{\vec {x}}\cdot {\vec {x}}}}={\sqrt {{x_{1}}^{2}+{x_{2}}^{2}+\dots +{x_{n}}^{2}}}} Обчислення кута ред. В евклідовому просторі виконується така рівність:
x → ⋅ y → = | x → | | y → | cos ∡ ( x → , y → ) {\displaystyle {\vec {x}}\cdot {\vec {y}}=|{\vec {x}}||{\vec {y}}|\cos \measuredangle \left({\vec {x}},{\vec {y}}\right)} На основі цього можна обчислити кут між векторами:
∡ ( x → , y → ) = arccos x → ⋅ y → | x → | | y → | {\displaystyle \measuredangle \left({\vec {x}},{\vec {y}}\right)=\arccos {\frac {{\vec {x}}\cdot {\vec {y}}}{\left|{\vec {x}}\right|\,\left|{\vec {y}}\right|}}} Визначення стандартного скалярного добутку в просторі комплексних векторів ред. Для C n {\displaystyle \mathbb {C} ^{n}} векторного простору над полем комплексних чисел стандартний скалярний добуток векторів x → , y → ∈ C n {\displaystyle {\vec {x}},{\vec {y}}\in \mathbb {C} ^{n}} відображення , що задовільняє наступним умовам:
x → ⋅ y → := ∑ i = 1 n x i y i ¯ = x 1 y 1 ¯ + x 2 y 2 ¯ + ⋯ + x n y n ¯ , {\displaystyle {\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}x_{i}{\overline {y_{i}}}={x_{1}}{\overline {y_{1}}}+{x_{2}}{\overline {y_{2}}}+\dotsb +{x_{n}}{\overline {y_{n}}},} де риска над комплексним числом позначає комплексно-спряжене число .
Інший варіант скалярного добутку можна визначити як
x → ⋅ y → := ∑ i = 1 n x i ¯ y i = x 1 ¯ y 1 + x 2 ¯ y 2 + ⋯ + x n ¯ y n {\displaystyle {\vec {x}}\cdot {\vec {y}}:=\sum _{i=1}^{n}{\overline {x_{i}}}y_{i}={\overline {x_{1}}}{y_{1}}+{\overline {x_{2}}}{y_{2}}+\dotsb +{\overline {x_{n}}}{y_{n}}} Таке визначення здебільшого використовується в фізиці.
Результати обох визначень є взаємно-спряженими комплексними числами. Для скалярного добутку вектора на самого себе, який визначає норму вектора, обидва визначення дають однаковий результат.
Властивості ред. Попри те, що у випадку дійсних чисел є симетричним, тобто x → ⋅ y → = y → ⋅ x → {\displaystyle {\vec {x}}\cdot {\vec {y}}={\vec {y}}\cdot {\vec {x}}} ермітовим , тобто x → ⋅ y → = y → ⋅ x → ¯ {\displaystyle {\vec {x}}\cdot {\vec {y}}={\overline {{\vec {y}}\cdot {\vec {x}}}}} Скалярний добуток не асоціативний (і не може бути, оскільки результатом скалярного добутку є скаляр, а не вектор). Скалярний добуток дистрибутивний стосовно додавання та віднімання . В евклідовому просторі спряженим стосовно лінійного оператора A {\displaystyle A} A ∗ {\displaystyle A^{*}} ⟨ A ⋅ x , y ⟩ = ⟨ x , A ∗ ⋅ y ⟩ {\displaystyle \langle A\cdot x,y\rangle =\langle x,A^{*}\cdot y\rangle } x {\displaystyle x} y {\displaystyle y} [2] Узагальнене визначення ред.
Якщо L {\displaystyle L} K {\displaystyle {\mathcal {K}}} L ¯ {\displaystyle {\overline {L}}} L {\displaystyle L} білінійне відображення L × L → K {\displaystyle L\times L\to {\mathcal {K}}} K = C {\displaystyle {\mathcal {K}}=\mathbb {C} } L × L ¯ → K {\displaystyle L\times {\overline {L}}\to {\mathcal {K}}} скалярним добутком .[3]
Скалярний добуток в дійсному векторному просторі V {\displaystyle V} білінійне відображення ⟨ ⋅ , ⋅ ⟩ : V × V → R {\displaystyle \langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {R} } x , y , z ∈ V {\displaystyle x,y,z\in V} λ ∈ R {\displaystyle \lambda \in \mathbb {R} } білінійність: ⟨ x + y , z ⟩ = ⟨ x , z ⟩ + ⟨ y , z ⟩ {\displaystyle \langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle } ⟨ x , y + z ⟩ = ⟨ x , y ⟩ + ⟨ x , z ⟩ {\displaystyle \langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle } ⟨ x , λ y ⟩ = λ ⟨ x , y ⟩ = ⟨ λ x , y ⟩ {\displaystyle \langle x,\lambda y\rangle =\lambda \langle x,y\rangle =\langle \lambda x,y\rangle } симетричність: ⟨ x , y ⟩ = ⟨ y , x ⟩ {\displaystyle \langle x,y\rangle =\langle y,x\rangle } додатньовизначеність: ⟨ x , x ⟩ ≥ 0 , {\displaystyle \langle x,x\rangle \geq 0,} ⟨ x , x ⟩ = 0 {\displaystyle \langle x,x\rangle =0} x = 0 {\displaystyle x=0} Скалярний добуток в комплексному векторному просторі V {\displaystyle V} півторалінійне відображення ⟨ ⋅ , ⋅ ⟩ : V × V → C {\displaystyle \langle {\cdot },{\cdot }\rangle \colon V\times V\to \mathbb {C} } x , y , z ∈ V {\displaystyle x,y,z\in V} λ ∈ C {\displaystyle \lambda \in \mathbb {C} } півторалінійність: ⟨ x + y , z ⟩ = ⟨ x , z ⟩ + ⟨ y , z ⟩ {\displaystyle \langle x+y,z\rangle =\langle x,z\rangle +\langle y,z\rangle } ⟨ x , y + z ⟩ = ⟨ x , y ⟩ + ⟨ x , z ⟩ {\displaystyle \langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle } ⟨ λ x , y ⟩ = λ ⟨ x , y ⟩ = ⟨ x , λ ¯ y ⟩ {\displaystyle \langle \lambda x,y\rangle =\lambda \langle x,y\rangle =\langle x,{\bar {\lambda }}y\rangle } ермітовість: ⟨ x , y ⟩ = ⟨ y , x ⟩ ¯ {\displaystyle \langle x,y\rangle ={\overline {\langle y,x\rangle }}} додатньовизначеність: ⟨ x , x ⟩ ≥ 0 {\displaystyle \langle x,x\rangle \geq 0} ⟨ x , x ⟩ = 0 {\displaystyle \langle x,x\rangle =0} x = 0 {\displaystyle x=0} ⟨ x , x ⟩ {\displaystyle \langle x,x\rangle } Дійсний або комплексний векторний простір, в якому визначено скалярний добуток, називається прегільбертовим.
Представлення у вигляді добутку матриць ред.
Стандартний скалярний добуток можна представити як добуток матриць . Водночас вектор представляється у вигляді матриці-стовпчика.
У випадку дійсних чисел, скалярний добуток представляється як:
⟨ x , y ⟩ = x T y = y T x {\displaystyle \langle x,y\rangle =x^{T}y=y^{T}x} де знаком T {\displaystyle {}^{T}} транспонування матриці .
У випадку комплексних чисел виконується:
⟨ x , y ⟩ = x ∗ y {\displaystyle \langle x,y\rangle =x^{*}y} де знаком ∗ {\displaystyle {}^{*}} ермітово-спряжена матриця .
Взагалі кажучи, у випадку дійсних чисел, кожна симетрична та додатноозначена матриця A {\displaystyle A}
⟨ x , y ⟩ A = x T A y {\displaystyle \langle x,y\rangle _{A}=x^{T}Ay} аналогічно, у випадку комплексних чисел кожна ермітова додатноозначена матриця A {\displaystyle A}
⟨ x , y ⟩ A = x ∗ A y {\displaystyle \langle x,y\rangle _{A}=x^{*}Ay} Див. також ред. Примітки ред. Література ред. Посилання ред. 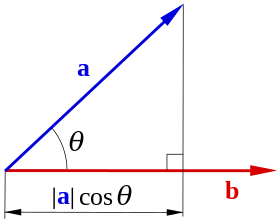
і

.
, де
— елемент Матриці Грама
,
.
.
.
.


.
, у випадку комплексних чисел є ермітовим, тобто
.
називається оператор
, для якого виконується рівність:
для довільних
,
.[2]







, це симетричне додатньовизначене білінійне відображення
, тобто, для
та
виконуються такі умови:
та
якщо
, це ермітове додатньовизначене півторалінійне відображення
, тобто, для
і
виконуються такі умови:
і
, якщо
. (те, що
дійсний, витікає з умови 2)
,

,


;

.
























