Ant colony optimization algorithms

In the natural world, ants of some species (initially) wander randomly, and upon finding food return to their colony while laying down pheromone trails. If other ants find such a path, they are likely not to keep travelling at random, but instead to follow the trail, returning and reinforcing it if they eventually find food (see Ant communication).^[9]

Over time, however, the pheromone trail starts to evaporate, thus reducing its attractive strength. The more time it takes for an ant to travel down the path and back again, the more time the pheromones have to evaporate. A short path, by comparison, gets marched over more frequently, and thus the pheromone density becomes higher on shorter paths than longer ones. Pheromone evaporation also has the advantage of avoiding the convergence to a locally optimal solution. If there were no evaporation at all, the paths chosen by the first ants would tend to be excessively attractive to the following ones. In that case, the exploration of the solution space would be constrained. The influence of pheromone evaporation in real ant systems is unclear, but it is very important in artificial systems.^[10]

The overall result is that when one ant finds a good (i.e., short) path from the colony to a food source, other ants are more likely to follow that path, and positive feedback eventually leads to many ants following a single path. The idea of the ant colony algorithm is to mimic this behavior with "simulated ants" walking around the graph representing the problem to solve.

New concepts are required since “intelligence” is no longer centralized but can be found throughout all minuscule objects. Anthropocentric concepts have been known to lead to the production of IT systems in which data processing, control units and calculating forces are centralized. These centralized units have continually increased their performance and can be compared to the human brain. The model of the brain has become the ultimate vision of computers. Ambient networks of intelligent objects and, sooner or later, a new generation of information systems that are even more diffused and based on nanotechnology, will profoundly change this concept. Small devices that can be compared to insects do not dispose of a high intelligence on their own. Indeed, their intelligence can be classed as fairly limited. It is, for example, impossible to integrate a high performance calculator with the power to solve any kind of mathematical problem into a biochip that is implanted into the human body or integrated in an intelligent tag which is designed to trace commercial articles. However, once those objects are interconnected they dispose of a form of intelligence that can be compared to a colony of ants or bees. In the case of certain problems, this type of intelligence can be superior to the reasoning of a centralized system similar to the brain.^[11]

Nature offers several examples of how minuscule organisms, if they all follow the same basic rule, can create a form of collective intelligence on the macroscopic level. Colonies of social insects perfectly illustrate this model which greatly differs from human societies. This model is based on the co-operation of independent units with simple and unpredictable behavior.^[12] They move through their surrounding area to carry out certain tasks and only possess a very limited amount of information to do so. A colony of ants, for example, represents numerous qualities that can also be applied to a network of ambient objects. Colonies of ants have a very high capacity to adapt themselves to changes in the environment as well as an enormous strength in dealing with situations where one individual fails to carry out a given task. This kind of flexibility would also be very useful for mobile networks of objects which are perpetually developing. Parcels of information that move from a computer to a digital object behave in the same way as ants would do. They move through the network and pass from one knot to the next with the objective of arriving at their final destination as quickly as possible.^[13]

Pheromone-based communication is one of the most effective ways of communication which is widely observed in nature. Pheromone is used by social insects such asbees, ants and termites; both for inter-agent and agent-swarm communications. Due to its feasibility, artificial pheromones have been adopted in multi-robot and swarm robotic systems. Pheromone-based communication was implemented by different means such as chemical ^[14][15][16] or physical (RFID tags,^[17] light,^{[18][19][20][21]} sound^[22]) ways. However, those implementations were not able to replicate all the aspects of pheromones as seen in nature.

Using projected light was presented in an 2007 IEEE paper by Garnier, Simon, et al. as an experimental setup to study pheromone-based communication with micro autonomous robots.^[23] Another study presented a system in which pheromones were implemented via a horizontal LCD screen on which the robots moved, with the robots having downward facing light sensors to register the patterns beneath them.^[24][25]

In the ant colony optimization algorithms, an artificial ant is a simple computational agent that searches for good solutions to a given optimization problem. To apply an ant colony algorithm, the optimization problem needs to be converted into the problem of finding the shortest path on a weighted graph. In the first step of each iteration, each ant stochastically constructs a solution, i.e. the order in which the edges in the graph should be followed. In the second step, the paths found by the different ants are compared. The last step consists of updating the pheromone levels on each edge.

procedure ACO_MetaHeuristic is    while not terminated do        generateSolutions()        daemonActions()        pheromoneUpdate()    repeatend procedure

Each ant needs to construct a solution to move through the graph. To select the next edge in its tour, an ant will consider the length of each edge available from its current position, as well as the corresponding pheromone level. At each step of the algorithm, each ant moves from a state ${\displaystyle x}$ to state ${\displaystyle y}$ , corresponding to a more complete intermediate solution. Thus, each ant ${\displaystyle k}$ computes a set ${\displaystyle A_{k}(x)}$ of feasible expansions to its current state in each iteration, and moves to one of these in probability. For ant ${\displaystyle k}$ , the probability ${\displaystyle p_{xy}^{k}}$ of moving from state ${\displaystyle x}$ to state ${\displaystyle y}$ depends on the combination of two values, the attractiveness ${\displaystyle \eta _{xy}}$ of the move, as computed by some heuristic indicating the a priori desirability of that move and the trail level ${\displaystyle \tau _{xy}}$ of the move, indicating how proficient it has been in the past to make that particular move. The trail level represents a posteriori indication of the desirability of that move.

In general, the ${\displaystyle k}$ th ant moves from state ${\displaystyle x}$ to state ${\displaystyle y}$ with probability

${\displaystyle p_{xy}^{k}={\frac {(\tau _{xy}^{\alpha })(\eta _{xy}^{\beta })}{\sum _{z\in \mathrm {allowed} _{y}}(\tau _{xz}^{\alpha })(\eta _{xz}^{\beta })}}}$

where ${\displaystyle \tau _{xy}}$ is the amount of pheromone deposited for transition from state ${\displaystyle x}$ to ${\displaystyle y}$ , ${\displaystyle \alpha }$ ≥ 0 is a parameter to control the influence of ${\displaystyle \tau _{xy}}$ , ${\displaystyle \eta _{xy}}$ is the desirability of state transition ${\displaystyle xy}$ (a priori knowledge, typically ${\displaystyle 1/d_{xy}}$ , where ${\displaystyle d}$ is the distance) and ${\displaystyle \beta }$ ≥ 1 is a parameter to control the influence of ${\displaystyle \eta _{xy}}$ . ${\displaystyle \tau _{xz}}$ and ${\displaystyle \eta _{xz}}$ represent the trail level and attractiveness for the other possible state transitions.

Trails are usually updated when all ants have completed their solution, increasing or decreasing the level of trails corresponding to moves that were part of "good" or "bad" solutions, respectively. An example of a global pheromone updating rule is

${\displaystyle \tau _{xy}\leftarrow (1-\rho )\tau _{xy}+\sum _{k}^{m}\Delta \tau _{xy}^{k}}$

where ${\displaystyle \tau _{xy}}$ is the amount of pheromone deposited for a state transition ${\displaystyle xy}$ , ${\displaystyle \rho }$ is the pheromone evaporation coefficient, ${\displaystyle m}$ is the number of ants and ${\displaystyle \Delta \tau _{xy}^{k}}$ is the amount of pheromone deposited by ${\displaystyle k}$ th ant, typically given for a TSP problem (with moves corresponding to arcs of the graph) by

${\displaystyle \Delta \tau _{xy}^{k}={\begin{cases}Q/L_{k}&{\mbox{if ant }}k{\mbox{ uses curve }}xy{\mbox{ in its tour}}\\0&{\mbox{otherwise}}\end{cases}}}$

where ${\displaystyle L_{k}}$ is the cost of the ${\displaystyle k}$ th ant's tour (typically length) and ${\displaystyle Q}$ is a constant.

Here are some of the most popular variations of ACO algorithms.

The ant system is the first ACO algorithm. This algorithm corresponds to the one presented above. It was developed by Dorigo.^[26]

In the ant colony system algorithm, the original ant system was modified in three aspects:

1. The edge selection is biased towards exploitation (i.e. favoring the probability of selecting the shortest edges with a large amount of pheromone);
2. While building a solution, ants change the pheromone level of the edges they are selecting by applying a local pheromone updating rule;
3. At the end of each iteration, only the best ant is allowed to update the trails by applying a modified global pheromone updating rule.^[27]

In this algorithm, the global best solution deposits pheromone on its trail after every iteration (even if this trail has not been revisited), along with all the other ants. The elitist strategy has as its objective directing the search of all ants to construct a solution to contain links of the current best route.

This algorithm controls the maximum and minimum pheromone amounts on each trail. Only the global best tour or the iteration best tour are allowed to add pheromone to its trail. To avoid stagnation of the search algorithm, the range of possible pheromone amounts on each trail is limited to an interval [τ_max,τ_min]. All edges are initialized to τ_max to force a higher exploration of solutions. The trails are reinitialized to τ_max when nearing stagnation.^[28]

All solutions are ranked according to their length. Only a fixed number of the best ants in this iteration are allowed to update their trials. The amount of pheromone deposited is weighted for each solution, such that solutions with shorter paths deposit more pheromone than the solutions with longer paths.

An ant colony system (ACS) with communication strategies is developed. The artificial ants are partitioned into several groups. Seven communicationmethods for updating the pheromone level between groups in ACS are proposed and work on the traveling salesman problem.^[29]

The pheromone deposit mechanism of COAC is to enable ants to search for solutions collaboratively and effectively. By using an orthogonal design method, ants in the feasible domain can explore their chosen regions rapidly and efficiently, with enhanced global search capability and accuracy. The orthogonal design method and the adaptive radius adjustment method can also be extended to other optimization algorithms for delivering wider advantages in solving practical problems.^[30]

It is a recursive form of ant system which divides the whole search domain into several sub-domains and solves the objective on these subdomains.^[31] The results from all the subdomains are compared and the best few of them are promoted for the next level. The subdomains corresponding to the selected results are further subdivided and the process is repeated until an output of desired precision is obtained. This method has been tested on ill-posed geophysical inversion problems and works well.^[32]

For some versions of the algorithm, it is possible to prove that it is convergent (i.e., it is able to find the global optimum in finite time). The first evidence of convergence for an ant colony algorithm was made in 2000, the graph-based ant system algorithm, and later on for the ACS and MMAS algorithms. Like most metaheuristics, it is very difficult to estimate the theoretical speed of convergence. A performance analysis of a continuous ant colony algorithm with respect to its various parameters (edge selection strategy, distance measure metric, and pheromone evaporation rate) showed that its performance and rate of convergence are sensitive to the chosen parameter values, and especially to the value of the pheromone evaporation rate.^[33] In 2004, Zlochin and his colleagues^[34] showed that COAC-type algorithms could be assimilated methods of stochastic gradient descent, on the cross-entropy and estimation of distribution algorithm. They proposed these metaheuristics as a "research-based model".

Ant colony optimization algorithms have been applied to many combinatorial optimization problems, ranging from quadratic assignment to protein folding or routing vehicles and a lot of derived methods have been adapted to dynamic problems in real variables, stochastic problems, multi-targets and parallel implementations.It has also been used to produce near-optimal solutions to the travelling salesman problem. They have an advantage over simulated annealing and genetic algorithm approaches of similar problems when the graph may change dynamically; the ant colony algorithm can be run continuously and adapt to changes in real time. This is of interest in network routing and urban transportation systems.

The first ACO algorithm was called the ant system^[26] and it was aimed to solve the travelling salesman problem, in which the goal is to find the shortest round-trip to link a series of cities. The general algorithm is relatively simple and based on a set of ants, each making one of the possible round-trips along the cities. At each stage, the ant chooses to move from one city to another according to some rules:

1. It must visit each city exactly once;
2. A distant city has less chance of being chosen (the visibility);
3. The more intense the pheromone trail laid out on an edge between two cities, the greater the probability that that edge will be chosen;
4. Having completed its journey, the ant deposits more pheromones on all edges it traversed, if the journey is short;
5. After each iteration, trails of pheromones evaporate.

• Sequential ordering problem (SOP) ^[35]
• Job-shop scheduling problem (JSP)^[36]
• Open-shop scheduling problem (OSP)^[37][38]
• Permutation flow shop problem (PFSP)^[39]
• Single machine total tardiness problem (SMTTP)^[40]
• Single machine total weighted tardiness problem (SMTWTP)^[41][42][43]
• Resource-constrained project scheduling problem (RCPSP)^[44]
• Group-shop scheduling problem (GSP)^[45]
• Single-machine total tardiness problem with sequence dependent setup times (SMTTPDST)^[46]
• Multistage flowshop scheduling problem (MFSP) with sequence dependent setup/changeover times^[47]
• Assembly Sequence Planning (ASP) problems^[48]

• Capacitated vehicle routing problem (CVRP)^[49][50][51]
• Multi-depot vehicle routing problem (MDVRP)^[52]
• Period vehicle routing problem (PVRP)^[53]
• Split delivery vehicle routing problem (SDVRP)^[54]
• Stochastic vehicle routing problem (SVRP)^[55]
• Vehicle routing problem with pick-up and delivery (VRPPD)^[56][57]
• Vehicle routing problem with time windows (VRPTW)^{[58][59][60][61]}
• Time dependent vehicle routing problem with time windows (TDVRPTW)^[62]
• Vehicle routing problem with time windows and multiple service workers (VRPTWMS)

• Quadratic assignment problem (QAP)^[63]
• Generalized assignment problem (GAP)^[64][65]
• Frequency assignment problem (FAP)^[66]
• Redundancy allocation problem (RAP)^[67]

• Set cover problem (SCP)^[68][69]
• Partition problem (SPP)^[70]
• Weight constrained graph tree partition problem (WCGTPP)^[71]
• Arc-weighted l-cardinality tree problem (AWlCTP)^[72]
• Multiple knapsack problem (MKP)^[73]
• Maximum independent set problem (MIS)^[74]

• Ant colony optimization (ACO) based optimization of 45 nm CMOS-based sense amplifier circuit could converge to optimal solutions in very minimal time.^[75]
• Ant colony optimization (ACO) based reversible circuit synthesis could improve efficiency significantly.^[76]

To optimize the form of antennas, ant colony algorithms can be used. As example can be considered antennas RFID-tags based on ant colony algorithms (ACO),^[78] loopback and unloopback vibrators 10×10^[77]

The ACO algorithm is used in image processing for image edge detection and edge linking.^[79][80]

• Edge detection:

The graph here is the 2-D image and the ants traverse from one pixel depositing pheromone. The movement of ants from one pixel to another is directed by the local variation of the image's intensity values. This movement causes the highest density of the pheromone to be deposited at the edges.

The following are the steps involved in edge detection using ACO:^[81][82][83]

Step 1: Initialization. Randomly place ${\displaystyle K}$ ants on the image ${\displaystyle I_{M_{1}M_{2}}}$ where ${\displaystyle K=(M_{1}*M_{2})^{\tfrac {1}{2}}}$ . Pheromone matrix ${\displaystyle \tau _{(i,j)}}$ are initialized with a random value. The major challenge in the initialization process is determining the heuristic matrix.

There are various methods to determine the heuristic matrix. For the below example the heuristic matrix was calculated based on the local statistics:the local statistics at the pixel position ${\displaystyle (i,j)}$ .

${\displaystyle \eta _{(i,j)}={\tfrac {1}{Z}}*Vc*I_{(i,j)},}$

where ${\displaystyle I}$ is the image of size ${\displaystyle M_{1}*M_{2}}$ ,

${\displaystyle Z=\sum _{i=1:M_{1}}\sum _{j=1:M_{2}}Vc(I_{i,j})}$

is a normalization factor, and

${\displaystyle {\begin{aligned}Vc(I_{i,j})=&f\left(\left\vert I_{(i-2,j-1)}-I_{(i+2,j+1)}\right\vert +\left\vert I_{(i-2,j+1)}-I_{(i+2,j-1)}\right\vert \right.\\&+\left\vert I_{(i-1,j-2)}-I_{(i+1,j+2)}\right\vert +\left\vert I_{(i-1,j-1)}-I_{(i+1,j+1)}\right\vert \\&+\left\vert I_{(i-1,j)}-I_{(i+1,j)}\right\vert +\left\vert I_{(i-1,j+1)}-I_{(i-1,j-1)}\right\vert \\&+\left.\left\vert I_{(i-1,j+2)}-I_{(i-1,j-2)}\right\vert +\left\vert I_{(i,j-1)}-I_{(i,j+1)}\right\vert \right)\end{aligned}}}$

${\displaystyle f(\cdot )}$ can be calculated using the following functions:

${\displaystyle f(x)=\lambda x,\quad {\text{for x ≥ 0; (1)}}}$

${\displaystyle f(x)=\lambda x^{2},\quad {\text{for x ≥ 0; (2)}}}$

${\displaystyle f(x)={\begin{cases}\sin({\frac {\pi x}{2\lambda }}),&{\text{for 0 ≤ x ≤}}\lambda {\text{; (3)}}\\0,&{\text{else}}\end{cases}}}$

${\displaystyle f(x)={\begin{cases}\pi x\sin({\frac {\pi x}{2\lambda }}),&{\text{for 0 ≤ x ≤}}\lambda {\text{; (4)}}\\0,&{\text{else}}\end{cases}}}$

The parameter ${\displaystyle \lambda }$ in each of above functions adjusts the functions’ respective shapes.

Step 2: Construction process. The ant's movement is based on 4-connected pixels or 8-connected pixels. The probability with which the ant moves is given by the probability equation ${\displaystyle P_{x,y}}$

Step 3 and Step 5: Update process. The pheromone matrix is updated twice. in step 3 the trail of the ant (given by ${\displaystyle \tau _{(x,y)}}$ ) is updated where as in step 5 the evaporation rate of the trail is updated which is given by:

${\displaystyle \tau _{new}\leftarrow (1-\psi )\tau _{old}+\psi \tau _{0}}$ ,

where ${\displaystyle \psi }$ is the pheromone decay coefficient ${\displaystyle 0<\tau <1}$

Step 7: Decision process. Once the K ants have moved a fixed distance L for N iteration, the decision whether it is an edge or not is based on the threshold T on the pheromone matrixτ. Threshold for the below example is calculated based on Otsu's method.

Image edge detected using ACO: The images below are generated using different functions given by the equation (1) to (4).^[84]

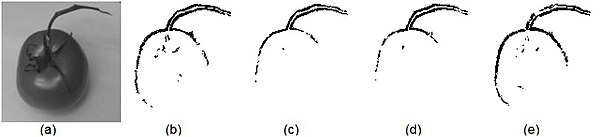
• Edge linking:^[85] ACO has also proven effective in edge linking algorithms.

• Bankruptcy prediction^[86]
• Classification^[87]
• Connection-oriented network routing^[88]
• Connectionless network routing^[89][90]
• Data mining^{[87][91][92][93]}
• Discounted cash flows in project scheduling^[94]
• Distributed information retrieval^[95][96]
• Energy and electricity network design^[97]
• Grid workflow scheduling problem^[98]
• Inhibitory peptide design for protein protein interactions^[99]
• Intelligent testing system^[100]
• Power electronic circuit design^[101]
• Protein folding^{[102][103][104]}
• System identification^[105][106]

With an ACO algorithm, the shortest path in a graph, between two points A and B, is built from a combination of several paths.^[107] It is not easy to give a precise definition of what algorithm is or is not an ant colony, because the definition may vary according to the authors and uses. Broadly speaking, ant colony algorithms are regarded as populated metaheuristics with each solution represented by an ant moving in the search space.^[108] Ants mark the best solutions and take account of previous markings to optimize their search. They can be seen as probabilistic multi-agent algorithms using a probability distribution to make the transition between each iteration.^[109] In their versions for combinatorial problems, they use an iterative construction of solutions.^[110] According to some authors, the thing which distinguishes ACO algorithms from other relatives (such as algorithms to estimate the distribution or particle swarm optimization) is precisely their constructive aspect. In combinatorial problems, it is possible that the best solution eventually be found, even though no ant would prove effective. Thus, in the example of the Travelling salesman problem, it is not necessary that an ant actually travels the shortest route: the shortest route can be built from the strongest segments of the best solutions. However, this definition can be problematic in the case of problems in real variables, where no structure of 'neighbours' exists. The collective behaviour of social insects remains a source of inspiration for researchers. The wide variety of algorithms (for optimization or not) seeking self-organization in biological systems has led to the concept of "swarm intelligence",^[11] which is a very general framework in which ant colony algorithms fit.

There is in practice a large number of algorithms claiming to be "ant colonies", without always sharing the general framework of optimization by canonical ant colonies.^[111] In practice, the use of an exchange of information between ants via the environment (a principle called "stigmergy") is deemed enough for an algorithm to belong to the class of ant colony algorithms. This principle has led some authors to create the term "value" to organize methods and behavior based on search of food, sorting larvae, division of labour and cooperative transportation.^[112]

Genetic algorithms (GA)

These maintain a pool of solutions rather than just one. The process of finding superior solutions mimics that of evolution, with solutions being combined or mutated to alter the pool of solutions, with solutions of inferior quality being discarded.

Estimation of distribution algorithm (EDA)

An evolutionary algorithm that substitutes traditional reproduction operators by model-guided operators. Such models are learned from the population by employing machine learning techniques and represented as probabilistic graphical models, from which new solutions can be sampled^[113][114] or generated from guided-crossover.^[115][116]

Simulated annealing (SA)

A related global optimization technique which traverses the search space by generating neighboring solutions of the current solution. A superior neighbor is always accepted. An inferior neighbor is accepted probabilistically based on the difference in quality and a temperature parameter. The temperature parameter is modified as the algorithm progresses to alter the nature of the search.

Reactive search optimization

Focuses on combining machine learning with optimization, by adding an internal feedback loop to self-tune the free parameters of an algorithm to the characteristics of the problem, of the instance, and of the local situation around the current solution.

Tabu search (TS)

Similar to simulated annealing in that both traverse the solution space by testing mutations of an individual solution. While simulated annealing generates only one mutated solution, tabu search generates many mutated solutions and moves to the solution with the lowest fitness of those generated. To prevent cycling and encourage greater movement through the solution space, a tabu list is maintained of partial or complete solutions. It is forbidden to move to a solution that contains elements of the tabu list, which is updated as the solution traverses the solution space.

Artificial immune system (AIS)

Modeled on vertebrate immune systems.

Particle swarm optimization (PSO)

A swarm intelligence method.

Intelligent water drops (IWD)

A swarm-based optimization algorithm based on natural water drops flowing in rivers

Gravitational search algorithm (GSA)

A swarm intelligence method.

Ant colony clustering method (ACCM)

A method that make use of clustering approach, extending the ACO.

Stochastic diffusion search (SDS)

An agent-based probabilistic global search and optimization technique best suited to problems where the objective function can be decomposed into multiple independent partial-functions.

Chronology of ACO algorithms

Chronology of ant colony optimization algorithms.

• 1959, Pierre-Paul Grassé invented the theory of stigmergy to explain the behavior of nest building in termites;^[117]
• 1983, Deneubourg and his colleagues studied the collective behavior of ants;^[118]
• 1988, and Moyson Manderick have an article on self-organization among ants;^[119]
• 1989, the work of Goss, Aron, Deneubourg and Pasteels on the collective behavior of Argentine ants, which will give the idea of ant colony optimization algorithms;^[120]
• 1989, implementation of a model of behavior for food by Ebling and his colleagues;^[121]
• 1991, M. Dorigo proposed the ant system in his doctoral thesis (which was published in 1992^[7]). A technical report extracted from the thesis and co-authored by V. Maniezzo and A. Colorni^[122] was published five years later;^[26]
• 1994, Appleby and Steward of British Telecommunications Plc published the first application to telecommunications networks^[123]
• 1995, Gambardella and Dorigo proposed ant-q,^[124] the preliminary version of ant colony system as first extension of ant system;.^[26]
• 1996, Gambardella and Dorigo proposed ant colony system ^[125]
• 1996, publication of the article on ant system;^[26]
• 1997, Dorigo and Gambardella proposed ant colony system hybridized with local search;^[27]
• 1997, Schoonderwoerd and his colleagues published an improved application to telecommunication networks;^[126]
• 1998, Dorigo launches first conference dedicated to the ACO algorithms;^[127]
• 1998, Stützle proposes initial parallel implementations;^[128]
• 1999, Gambardella, Taillard and Agazzi proposed macs-vrptw, first multi ant colony system applied to vehicle routing problems with time windows,^[58]
• 1999, Bonabeau, Dorigo and Theraulaz publish a book dealing mainly with artificial ants^[129]
• 2000, special issue of the Future Generation Computer Systems journal on ant algorithms^[130]
• 2000, Hoos and Stützle invent the max-min ant system;^[28]
• 2000, first applications to the scheduling, scheduling sequence and the satisfaction of constraints;
• 2000, Gutjahr provides the first evidence of convergence for an algorithm of ant colonies^[131]
• 2001, the first use of COA algorithms by companies (Eurobios and AntOptima);
• 2001, Iredi and his colleagues published the first multi-objective algorithm^[132]
• 2002, first applications in the design of schedule, Bayesian networks;
• 2002, Bianchi and her colleagues suggested the first algorithm for stochastic problem;^[133]
• 2004, Dorigo and Stützle publish the Ant Colony Optimization book with MIT Press ^[134]
• 2004, Zlochin and Dorigo show that some algorithms are equivalent to the stochastic gradient descent, the cross-entropy method and algorithms to estimate distribution^[34]
• 2005, first applications to protein folding problems.
• 2012, Prabhakar and colleagues publish research relating to the operation of individual ants communicating in tandem without pheromones, mirroring the principles of computer network organization. The communication model has been compared to the Transmission Control Protocol.^[135]
• 2016, first application to peptide sequence design.^[99]
• 2017, successful integration of the multi-criteria decision-making method PROMETHEE into the ACO algorithm (HUMANT algorithm).^[136]

• M. Dorigo, 1992. Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy.
• M. Dorigo, V. Maniezzo & A. Colorni, 1996. "Ant System: Optimization by a Colony of Cooperating Agents", IEEE Transactions on Systems, Man, and Cybernetics–Part B, 26 (1): 29–41.
• M. Dorigo & L. M. Gambardella, 1997. "Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem". IEEE Transactions on Evolutionary Computation, 1 (1): 53–66.
• M. Dorigo, G. Di Caro & L. M. Gambardella, 1999. "Ant Algorithms for Discrete Optimization Archived 2018-10-06 at the Wayback Machine". Artificial Life, 5 (2): 137–172.
• E. Bonabeau, M. Dorigo et G. Theraulaz, 1999. Swarm Intelligence: From Natural to Artificial Systems, Oxford University Press. ISBN 0-19-513159-2
• M. Dorigo & T. Stützle, 2004. Ant Colony Optimization, MIT Press. ISBN 0-262-04219-3
• M. Dorigo, 2007. "Ant Colony Optimization". Scholarpedia.
• C. Blum, 2005 "Ant colony optimization: Introduction and recent trends". Physics of Life Reviews, 2: 353-373
• M. Dorigo, M. Birattari & T. Stützle, 2006 Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. TR/IRIDIA/2006-023
• Mohd Murtadha Mohamad,"Articulated Robots Motion Planning Using Foraging Ant Strategy", Journal of Information Technology - Special Issues in Artificial Intelligence, Vol. 20, No. 4 pp. 163–181, December 2008, ISSN 0128-3790.
• N. Monmarché, F. Guinand & P. Siarry (eds), "Artificial Ants", August 2010 Hardback 576 pp. ISBN 978-1-84821-194-0.
• A. Kazharov, V. Kureichik, 2010. "Ant colony optimization algorithms for solving transportation problems", Journal of Computer and Systems Sciences International, Vol. 49. No. 1. pp. 30–43.
• C-M. Pintea, 2014, Advances in Bio-inspired Computing for Combinatorial Optimization Problem, Springer ISBN 978-3-642-40178-7
• K. Saleem, N. Fisal, M. A. Baharudin, A. A. Ahmed, S. Hafizah and S. Kamilah, "Ant colony inspired self-optimized routing protocol based on cross layer architecture for wireless sensor networks", WSEAS Trans. Commun., vol. 9, no. 10, pp. 669–678, 2010. ISBN 978-960-474-200-4
• K. Saleem and N. Fisal, "Enhanced Ant Colony algorithm for self-optimized data assured routing in wireless sensor networks", Networks (ICON) 2012 18th IEEE International Conference on, pp. 422–427. ISBN 978-1-4673-4523-1
• Abolmaali S, Roodposhti FR. Portfolio Optimization Using Ant Colony Method a Case Study on Tehran Stock Exchange. Journal of Accounting. 2018 Mar;8(1).

• Scholarpedia Ant Colony Optimization page
• Ant Colony Optimization Home Page
• "Ant Colony Optimization" - Russian scientific and research community
• AntSim - Simulation of Ant Colony Algorithms
• MIDACO-Solver General purpose optimization software based on ant colony optimization (Matlab, Excel, VBA, C/C++, R, C#, Java, Fortran and Python)
• University of Kaiserslautern, Germany, AG Wehn: Ant Colony Optimization Applet Visualization of Traveling Salesman solved by ant system with numerous options and parameters (Java Applet)
• Ant algorithm simulation (Java Applet)
• Java Ant Colony System Framework
• Ant Colony Optimization Algorithm Implementation (Python Notebook)